fibonacci数列(二)
时间限制: 1000 ms | 内存限制: 65535 KB
难度: 3
- 描述
-
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula for the Fibonacci sequence is
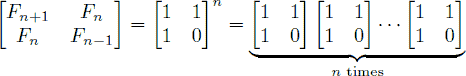 .
.Given an integer n, your goal is to compute the last 4 digits of Fn.
Hint
As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by
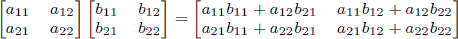 .
.Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:
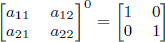 .
.
- 输入
- The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1. 输出
- For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000). 样例输入
-
091000000000-1
样例输出 -
0346875

 View Code
View Code 1 2 #include
3 #define N 20000 4 int f[N]={ 0,1}; 5 int findT() 6 { 7 int i,j,k; 8 for(i=2;i